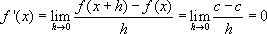2014年11月9日 星期日
2014年11月6日 星期四
log7 怎麼算
已知 log 2 = 0.3010, log 3 = 0.4771, 如何預估 log 7
第一步 : 算出其他值 :
log 4=log(2^2)=2log 2=0.6020
log 5=log(10/2)=log10-log2=1-0.3010=0.6990
log 6=log(2*3)=log2+log3=0.7781
log 7
log 8=log(2^3)=3log2=0.9030
log 9=log(3^2)=2log3=0.9541
log10=1
第二步 : 多次線性差分
得6x-5.0713 ~= 3.3797-4x,
x ~=8.4510/10 ~= 0.8451
第一步 : 算出其他值 :
log 4=log(2^2)=2log 2=0.6020
log 5=log(10/2)=log10-log2=1-0.3010=0.6990
log 6=log(2*3)=log2+log3=0.7781
log 7
log 8=log(2^3)=3log2=0.9030
log 9=log(3^2)=2log3=0.9541
log10=1
第二步 : 多次線性差分
原函數(四次)
|
差分(三次函數)
|
二次差分(二次)
|
三次差分(線性)
|
四次差分(常數)
|
log 5=0.6990
|
(後項減前項)
| |||
log 6=0.7781
|
0.0791
|
(後項減前項)
| ||
log 7=x
|
x-0.7781
|
x-0.8572
|
(後項減前項)
| |
log 8=0.9030
|
0.9030-x
|
1.6811-2x
|
2.5383-3x
|
(後項減前項)
|
log 9=0.9541
|
0.0511
|
x-0.8519
|
3x-2.5330
|
6x-5.0713
|
log10=1
|
0.0459
|
-0.0052
|
0.8467-x
|
3.3797-4x
|
得6x-5.0713 ~= 3.3797-4x,
x ~=8.4510/10 ~= 0.8451
2014年9月27日 星期六
牛頓環 Newton's ring
http://zh.wikipedia.org/wiki/%E7%89%9B%E9%A0%93%E7%92%B0
將一塊平凸透鏡凸面朝下放在一塊平面透鏡上,將單色光直射向凸鏡的平面,可以觀察到一個個明暗相間的圓環條紋。
若使用白光,則可以觀察到彩虹狀的圓環彩色條紋。第一個對此現象進行分析的人是英國物理學家艾薩克·牛頓爵士,因而命名為牛頓環
http://baike.baidu.com/view/49777.htm?fr=iciba
將一塊平凸透鏡凸面朝下放在一塊平面透鏡上,將單色光直射向凸鏡的平面,可以觀察到一個個明暗相間的圓環條紋。
若使用白光,則可以觀察到彩虹狀的圓環彩色條紋。第一個對此現象進行分析的人是英國物理學家艾薩克·牛頓爵士,因而命名為牛頓環
http://baike.baidu.com/view/49777.htm?fr=iciba
2014年9月20日 星期六
階乘
定義: n! = n x (n-1) x (n-2) ... x 1
n 為正整數
=> f(x) = x * f(x-1)
擴展到 0 : 0! 為 1
f(1) = 1 * f(0)
Gamma 函數 : http://zh.wikipedia.org/wiki/%CE%93%E5%87%BD%E6%95%B0
微分 - 基本定律
定義:
法則:
href: http://webcai.math.fcu.edu.tw/calculus/calculus_html/3-3/law.htm
1. 常數微分 :
2.
證明:
3. 冪次定律:
證明: 假設n 為整數.
4.
證明:
5. 加法定律 :
證明:
6. 減法定律 :
7. 乘法定律 :
證明:
8. 除法定律 :
證明:
改變世界的17個方程式
勾股定理
又稱為商高定理, 畢達哥拉斯定理.
( ref: http://zh.wikipedia.org/wiki/%E5%8B%BE%E8%82%A1%E5%AE%9A%E7%90%86 )
- 平面上的直角三角形的兩條直角邊的長度(古稱勾長、股長)的平方和
等於 斜邊長(古稱弦長)的平方。
- 反之,若平面上三角形中兩邊長的平方和等於第三邊邊長的平方,則它是直角三角形
( ref: http://episte.math.ntu.edu.tw/articles/mm/mm_02_3_07/ )

--
證明方法二:
梯形方式
---
證明方式三: 弦圖
---
證明方式四: 相似三角形
射影定理
---
The Pythagorean Proposition: Elisha S. Loomis
The Pythagorean Theorem: A 4000-Year History - Eli Maor
( ref: http://zh.wikipedia.org/wiki/%E5%8B%BE%E8%82%A1%E5%AE%9A%E7%90%86 )
- 平面上的直角三角形的兩條直角邊的長度(古稱勾長、股長)的平方和
等於 斜邊長(古稱弦長)的平方。
- 反之,若平面上三角形中兩邊長的平方和等於第三邊邊長的平方,則它是直角三角形
( ref: http://episte.math.ntu.edu.tw/articles/mm/mm_02_3_07/ )
如設三角形 ABC 三個邊為 a,b,c,其中 c 為斜邊 (如圖一),則其間的關係為: a2 + b2 = c2。
圖一 |
證明方法一: 利用 代數平方公式
前提:
(1) 代數平方公式 : (a+b)2 = a2 + b2 + 2ab
前提:
(1) 代數平方公式 : (a+b)2 = a2 + b2 + 2ab
(2) 三角形內角和 : 平角(180 度 )
(3) 正方形 : 直角 (90 度)
(4) 三角形面積 : ab/2
(5) 正方形面積
(3) 正方形 : 直角 (90 度)
(4) 三角形面積 : ab/2
(5) 正方形面積
圖二 |
相同之四個直角三角形,我們很容易看出可接成如圖二之圖形,而形成一正方形,此正方形恰好是由原四個相同之直角三角形及一邊長為 c 的正方形所合成。當我們知道正方形的面積為一邊長的平方時,則有下列關係。
此處  表原直角三角形之面積,化簡上式,結果得:
表原直角三角形之面積,化簡上式,結果得:
a2 + b2 = c2 .
證明方法二:
梯形方式
---
證明方式三: 弦圖
---
證明方式四: 相似三角形
射影定理
(射影定理)
---
The Pythagorean Proposition: Elisha S. Loomis
The Pythagorean Theorem: A 4000-Year History - Eli Maor
訂閱:
意見 (Atom)
熱門文章
-
已知 log 2 = 0.3010, log 3 = 0.4771, 如何預估 log 7 第一步 : 算出其他值 : log 4=log(2^2)=2log 2=0.6020 log 5=log(10/2)=log10-log2=1-0.3010=0.6990 lo...
-
(By midjourney) cinematic photo still, glamour shot of a 20-year-old Japanese female model with sports wear running behind a huge turtle, c...